A conveyor, as its name suggests, is analogous to a conveyor belt, where material gets put on one end, then moves along with the conveyor belt, and then comes off the conveyor belt at the other end. The FIFO conveyor behaves the same as a conveyor belt, and also allows leakage from different locations on the conveyor.
Note that this material applies with the FIFO option for a conveyor is selected. If it is not selected then the discussion in Traditional Conveyor Computation applies
Note If the transit time is constant, a FIFO conveyor behaves identically with a non-FIFO conveyor.
FIFO Conveyors take on and release material every DT, with material moving along the length of the conveyor (assumed to be 1) over the specified transit time. The material is placed evenly over the beginning edge of the conveyor (the edge has a length of DT/transit_time). The material is taken off the other end of the conveyor (the last DT/transit_time of the conveyor) and this determines the outflow. If there are leakages then the material on the conveyor, including the material that will come off the conveyor, is decreased by the leakage where it sits on the conveyor.
Material comes from all of the inflows lumped together. The material may be heterogeneous (for example, when using cycle time (see Attribute and Cycle Time Tracking) there may be different time stamps from different inflows), but when computing volume of material everything is processed together.
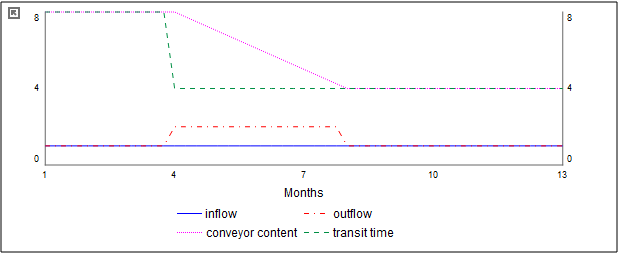
Since the conveyor is treated as if it has a unit length, the longer the delay time the smaller the portion of the conveyor a single DT worth of material will occupy. When the transit time decreases, the portion of the conveyor covered, and uncovered, in a single DT increases. This will result in an increased outflow until the material placed on the conveyor at the old transit time is exhausted.
The following illustrates the response to halving the transit time for a conveyor with a constant inflow:

The response occurs at the same time the transit time is changed, and the outflow is doubled until the material from the old transit time deposits is exhausted.
There are two types of leakage: linear and exponential. With linear leakage, the same amount is taken away every DT. For example, if the leak fraction was 8% (0.08) then 1% of the material would be taken out during each of the 8 DTs the material was in the conveyor. Thus a time lapsed picture of our material over the 8 DTs would look like:

Here the red indicates the quantity that will leak out when the conveyor advances. All of the leakages are the same size.
With exponential leakage, the same fraction of the material remaining is removed every DT. Thus if the leak rate were 0.4 (per month), 10% of the material would be removed each DT. Exponential leakage would look like:

Notice that the red is big at first, but gets smaller as it moves down the conveyor. The leakages are all the same proportion of the material in the conveyor sections.
The outflow from a conveyor is always the material at the end of the conveyor (the portion before 1 as labeled above. Leakages will already have been applied to the material in prior DTs, and will also be applied for the current DT. Leakages can make the outflow 0.
Note It is not possible to connect a conveyor outflow to something that would constrain the flow value. So the conveyor itself determines the value of the outflow.
Initialization is the same for FIFO and non FIFO conveyors and is described in Traditional Conveyor Computation.
Leakages are applied in the order they are drawn, with the first one connected to the stock having the highest priority. This priority is shown in the panel. To change the priority of leakages disconnect them, then reconnect them in a different order.
With linear leakages the total fraction leaking out can't exceed 1. With a leak fraction of 1, there will be no outflow. If the sum of the leak fractions over multiple leakages is larger than 1, the last, or later, leakages may get less than their leak fraction suggests, and may get nothing at all.
With exponential leakage all the leakages are computed always. If they are large, the amount of material in the conveyor will drain very quickly.
Note Leak fractions can change over time and the current values will be used when computing leakages.
Leakages can occur over the entire conveyor, or only over a portion of the conveyor. When using a linear leakage the total amount leaked will be the same regardless of the length of the leak zone (that is, the amount taken from the leak zone in each DT will be larger for a shorter leak zone). The leak zone is mapped to the unit length of the conveyor so that when transit time changes the age of leaked material will also change.
Linear: When there are different leak zones, the meaning of the leak fraction can refer to the inflowing quantity, or the amount remaining at the beginning of the leak zone, depending on the setting for Ignore losses from earlier leak zones in the Equation Tab of the properties panel.
If Ignore losses from earlier leak zones is not checked, then the leakage fraction applies to the amount of material at the start of the leak zone it is applied to. For example, if there is one leakage with a leak zone from 0 to 50, and a second with 50 to 100, the second leak fraction will be applied to the amount of material left when it has passed half way through the conveyor. Two 50% (0.5) leakages in this case would result in 75% (0.75) of the incoming material being removed so that only 25% flowed out.
Note If the transit time is variable then the total amount leaked may not follow the above formula.
If Ignore losses from earlier leak zones is checked, the leakage applies to the amount of material coming into the conveyor. Thus, in the above example, the first leakage would take 50%, and the second another 50% so the outflow would be 0.
Exponential:Leak zones turn on and off exponential leakage. If the leak zones overlap the leakage fractions will be added. In the above case (non overlapping leak zones covering the entire conveyor), if the leakage fraction were 0.1 for both leakages the conveyor would behave the same way it would with a single leakage of 0.1 over the full range.
When leaking integers the fractional amount of the leakage is computed and accumulated until it exceeds 1, then one unit of material is leaked (the amount leaked is the leakage flow multiplied by DT, so the leakage flow will be a multiple of 1/DT). The leakages can thus become uneven, and may not all be applied as the material may flow out with some fractional leakage already accumulated. In this case there will
Linear: The leak zone is always made relative to the unit conveyor length. If transit time decreases the leakage will need to be higher to ensure that the correct amount of leakage has occurred for material leaving the leak zone. If the transit time increases then less will leak out toward the end to ensure the total leakage is correct.
Exponential: Exponential bases leakage on the material in the conveyor. It will leak a fraction of that material regardless of where it is in the leak zone. With a full leak zone this means that the total leakage will be the amount in the conveyor multiplied by the leakage rate. Increasing or decreasing the transit time does not affect this computation except that the total amount of time spent in the conveyor (or a leak zone within the conveyor), and thus the total leakage, will change.