Trigonometric builtins perform basic trigonometric calculations. The trigonometric builtins can be useful in modeling scientific problems (for example, kinematics in two or three dimensions). They also can be helpful if you want to derive an input to the model using a periodically fluctuating signal (e.g., sine or cosine wave).
This section describes the following builtins:
The ARCCOS builtin gives the arccosine of expression. The arccosine is the angle, in radians, whose cosine is expression. The angle will be in the range 0 to p. To convert measurement between degrees and radians, use the identity:
p (radians) = 180 (degrees).
The expression value can be either a constant or a variable.
Examples:
ARCCOS(0.5) equals 1.047 (radians)
ARCCOS(0.5)*180/p equals 60 (degrees)
The ARCSIN builtin gives the arcsine of expression. The arcsine is the angle, in radians, whose sine is expression. The angle will be in the range -p/2 to p/2. To convert measurement between degrees and radians, use the identity:
p (radians) = 180 (degrees).
The expression value can be either a constant or a variable.
Examples:
ARCSIN(0.866) equals 1.047 (radians)
ARCSIN(0.866)*180/p equals 60 (degrees)
The ARCTAN builtin gives the arctangent of expression. The arctangent is the angle, in radians, whose tangent is expression. The angle will be in the range -p/2 to p/2. To convert measurement between degrees and radians, use the identity:
p (radians) = 180 (degrees).
The expression value can be either a constant or a variable.
Examples:
ARCTAN(1) equals 0.785 (p/4) (radians)
ARCTAN(1)*180/p equals 45 (degrees)
The COS builtin gives the cosine of radians, where radians is an angle in radians. To convert measurement between degrees and radians, use the identity:
p (radians) = 180 (degrees).
The radians value can be either a constant or a variable.
Examples:
COS(1.047) equals 0.5
COS(60*(p/180)) equals 0.5
The COSWAVE builtin returns a time-dependent cosine wave, with the specified amplitude and period. To generate the cosine wave, the COSWAVE builtin uses the absolute value of the amplitude you specify. To produce meaningful wave results, choose a DT that's significantly smaller than the period of the wave. A DT equal to a quarter of the period gives triangle waves. A smaller DT gives results which better approximate a continuous curve.
Examples:
COSWAVE(10,5) generates a cosine wave with an amplitude of 10 units and a period of 5 time units.
COSWAVE(-5,2) generates a cosine wave with an amplitude of 5 units and a period of 2 time units.
The SIN builtin gives the sine of radians, where radians is an angle in radians. To convert measurement between degrees and radians, use the identity:
p (radians) = 180 (degrees).
The radians value can be either a constant or a variable.
Examples:
SIN(1.047) equals 0.866
SIN(60*p/180) equals 0.866
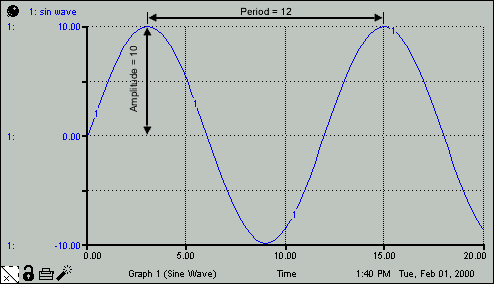
sin_wave = 10*SIN(2*p*TIME/12) generates a sinusoidal fluctuation with an amplitude of 10 and a period of 12, as shown in the following figure.

The SINWAVE builtin returns a time-dependent sine wave, with the specified amplitude and period. The SINWAVE builtin uses the absolute value of the amplitude you specify to generate the sine wave. To produce meaningful wave results, choose a DT that's significantly smaller than the period of the wave. A DT equal to a quarter of the period gives triangle waves. A smaller DT gives results which better approximate a continuous curve.
Examples:
SINWAVE(10,5) generates a sine wave with an amplitude of 10 units and a period of 5 time units.
SINWAVE(-5,2) generates a sine wave with an amplitude of 5 units and a period of 2 time units.
The TAN builtin gives the tangent of radians, where radians is an angle in radians. To convert measurement between degrees and radians, use the identity:
p (radians) = 180 (degrees).
The radians value can be either a constant or a variable.
Examples:
TAN(0.785) equals 1
TAN(45*p/180) equals 1