A conveyor, as its name suggests, is analogous to a conveyor belt, where material gets put on one end, then moves along with the conveyor belt, and then comes off the conveyor belt at the other end. Indeed, if there are no leakages and the transit time on the conveyor is constant, that is exactly what the conveyor does. If you add leakages or vary the transit time, the picture becomes a bit more complicated, but the analogy to a conveyor belt is still quite strong.
Conveyors take on and release material every DT, but in describing the way they work it is easiest to look at a single bunch of material put on during one DT and see how it get processed until it finally reaches the end of the conveyor. This bunch of material comes from all of the inflows lumped together. This lump could be heterogeneous (for example, when using cycle time (see Cycle-Time Introduction) Stella different time stamps within a slat), but we will just look at the volume of material as everything is processed together.
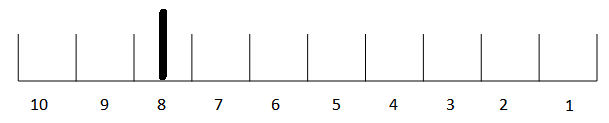
During the DT in which the material is placed on the conveyor the transit time is used to determine how far from the end (measured in time units) of the conveyor to place the material. It is placed in what is called a slat, which is just another name for one DTs worth of material. Suppose that at the conveyor has a transit time of 2 and DT is 1/4, then a flow computed at the previous DT would enter the conveyor as follows:

Here the numbers represent DTs until the material is released from the conveyor. If the transit time were shorter the lump would have been places to the right, longer to the left. Once it is placed, transit time has no effect on it. With no leakage, the next DT the state of the conveyor would be:
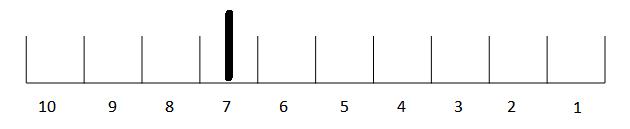
And so on until 8 DTs (2 time units) later when it would be:
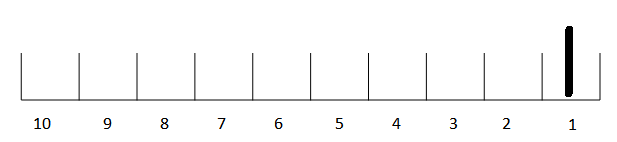
And then it would be empty, and the full amount of material that flowed in would be counted in the outflow.
If there is leakage, the same thing happens, but the last DT would look something like

and the times that preceded it, would all be larger until slat 8 which would match the no leakage case.
There are two types of leakage: linear and exponential. With linear leakage, the same amount is taken away every DT. For example if the leak fraction was 8% (0.08) then 1% of the material would be taken out during each of the 8 DTs the meterial was in the conveyor. Thus a time lapsed picture of our material over the 8 DTs would look like:
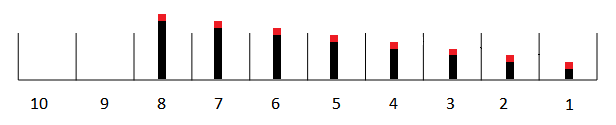
Here the red indicates the quantity that will leak out when moving to the next slat, or on exiting (so the black in slat 1 is the amount of the outflow). All of the leakages are the same size.
With exponential leakage, the same fraction of the material remaining is removed every DT. Thus if the leak rate were 0.4 (per month), 10% of the material would be removed each DT. Exponential leakage would look like:
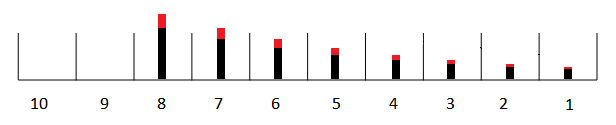
Notice that the red is big at first, but gets smaller as it moves from one slat to the next. The leakages are all the same proportion of the material in the slat.
Note It is the value of transit time at the DT when the conveyor gets the inflow that matters. If it changes after that it will only affect quantities of material received later.
Note If the transit time decreases, material added to a conveyor a later time may exit the conveyor at an earlier time (conveyors are not FIFO).
The outflow from a conveyor is always the material in the slat 1 as they are numbered above. Leakages will already have been applied to the material in prior DTs, and will also be applied for the current DT. Leakages can make the outflow 0.
Note It is not possible to connect a conveyor outflow to something that would constrain the flow value. So the conveyor itself determines the value of the outflow.
Leakages are applied in the order they are drawn, with the first one connected to the stock having the highest priority. This priority is shown in the panel. To change the priority of leakages disconnect them, then reconnect them in a different order.
With linear leakages the total fraction leaking out can't exceed 1. With a leak fraction of 1, there will be no outflow. If the sum of the leak fractions is larger than 1, the last, or later, leakages may get less than their leak fraction suggests, and may get nothing at all.
With exponential leakage all the leakages are computed always. If they are large, the amount of material in the conveyor will drain very quickly.
Note Leak fractions can change over time and the current values will be used when computing leakages.
When leaking integers the fractional amount of the leakage is computed and accumulated until it exceeds 1, then one unit of material is leaked. The leakages can thus become uneven, and may not all be applied as the material may flow out with some fractional leakage already accumulated.
You can explicitly initialize slats in a conveyor by using a comma separated list (semicolon separated if you use , for the decimal mark) of numbers. Each entry in the list corresponds to a time unit, and its value will be spread evenly over the slatss within a time unit. For example, in the above discussion specifying 4,8 would put 1 each in slats 1,2,3,4 and 2 each in slats 5,6,7,8 in the above example.
If you specify a number (or an expression) for the initial value Stella will attempt to start the internal workings of the conveyor in steady state. The slats to theleft (bigger numbers) will get more of the material, as it would be expected to leak out over time. The profiles for this initialization look very much like the examples given above.